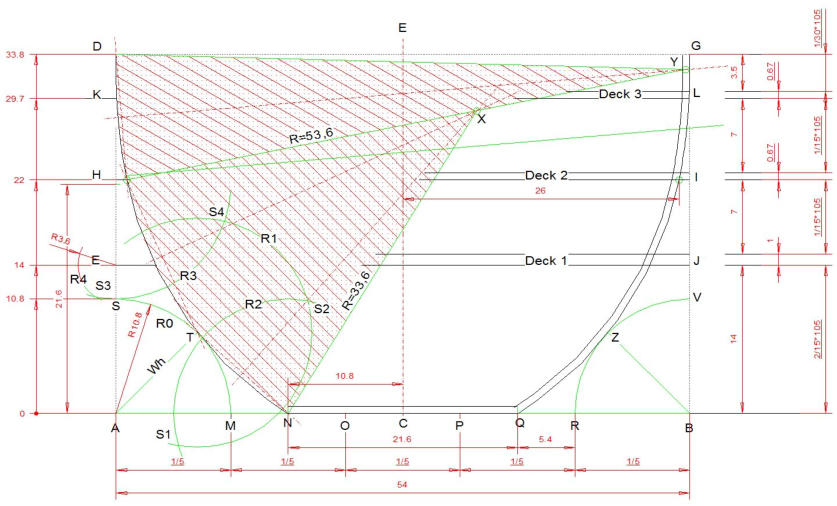
Die Weite des Flachs von 21,6 Palmi vertikal von A nach oben abtragen. Durch den neuen Schnittpunkt in der Nähe von H R3=R0 erstellen.
R4=1/3*R0=3,6 Palmi wird durch den Schnittpunkt E/Außenkante Schiffsweite auf der Höhe des Deck1 erzeugt.
Durch die gewonnenen Schnittpunkte S1, S2, S3, S4 sollte im Kreuzungspunkt der beiden Geraden die Spantkontur H-T-N entstehen. Der Mittelpunkt des unteren
Radius sollte Lavanha zufolge in X gefunden werden.
Lavanha bemerkte so ganz nebenbei, dass die Spantkontur wohl doch nicht aus nur einem Kreissegment bestand. Er erwähnte den Mittelpunkt Y für den oberen
Kreisbogen, der von H nach D gezogen werden sollte.
Leider konnte das so nicht umgesetzt werden. Die erzeugten Geraden trafen sich nicht an den gewünschten Stellen X und Y.
Diese, von Lavanha beschriebene Vorgehensweise konnte mit den heutigen technischen Mitteln nur beding nachvollzogen werden. Es war nicht möglich, den
Schnittpunkt der unteren Spantkontur eindeutig zu definieren. Der Kreisbogen konnte aber über drei Punkte N-T-H konstruiert werden und lieferte das gewünschte
Ergebnis. Der obere Kreisabschnitt H-K-D war dann leicht zu zeichnen, indem ein Kreissegment tangential an den Ersten angefügt wurde. Auch hier wurde über
drei Punkte der richtige Kreisbogen ermittelt.
Die von Lavanha eingezeichneten und beschriebenen Abrundungen bei N und Q wurden hier nicht berücksichtigt. Es ging um die Machbarkeit einer derartigen
Konstruktion, nicht um die Rekonstruktion eines Schiffes nach diesem hier vorgestellten Entwurfssystem.
Erst nach vielen Versuchen wurde deutlich, dass die aufwendige Konstruktion der Kreissegmente nicht der Findung der Spantkontur diente, sondern der beiden
notwendigen Senten. Der untere Schnittpunkte R1/Spantkontur und R3/Spantkontur definierten diese beiden Stellen. Ob Lavanha dieses bewusst verheimlichte,
oder es nicht genau wusste, lässt sich nicht mehr rekonstruieren. Die unvollständige Beschreibung der Senten deutet jedoch auf Letzteres hin.