Die Konstruktion des Achterstevens nach Lavanha
Im Vergleich zur Vorstevenkonstruktion ist die der Achterstevenkonstruktion
recht einfach gehalten. Seine Höhe A-C wurde aus 2/5*Kiellänge ermittelt. Der
Überhang C-D oder Stevenfall betrug hier 2/7*Achterstevenhöhe. In Maßen
ausgedrückt hatte der Steven eine Höhe von 2/5*105=42 Palmi und einen Fall
von 2/7*42=12 Palmi. Es ist wohl davon auszugehen, dass sich diese Maße
auf die Hinterkante des Stevens bezogen.


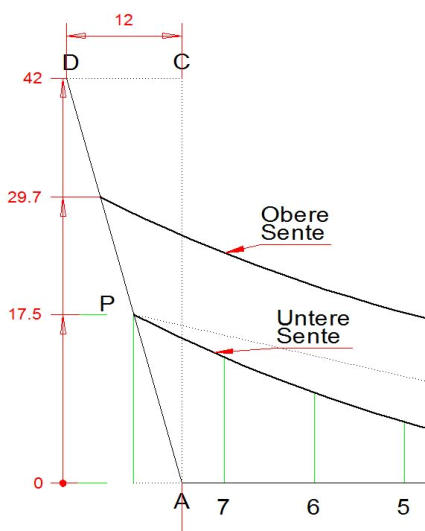
Der Querschnitt
Die Querschnittkonstruktion weicht doch erheblich von der englischen oder venezianischen Form und Vorgehensweise ab. Die Findung der beiden Radien war
wohl etwas aufwendig ins Bild gesetzt. Ein wichtiges Maß war die Schiffsweite, die in Höhe des dritten Decks im Raum gemessen wurde. Hierzu wollte Lavanha
die Kiellänge+Überhang Achtersteven+Überhang Vorsteven errechnet haben. Das Ergebnis betrug 152 Palmi. Zu diesem Maß kamen dann 1/3 der
Heckbalkenlänge mit 9 Palmi hinzu. Das Ergebnis von 161 Palmi musste dann noch durch 3 dividiert werden. Die erhoffte Schiffsweite sollte 54 Palmi betragen.
Nach heutiger Berechnung kommen wir nur auf 53,666667 Palmi. Es fehlen also noch 0,333333 Palmi. Der Autor Lavanha löste dieses Problem dadurch, dass er
den Wert 152 Palmi um einen Palmo auf 153 Palmi erhöhte. Das Ergebnis der erneuten Berechnung ergab dann 162 Palmi. Dividiert durch 3, bekam man dann
die gewünschten 54 Palmi für die Schiffsweite.
Eine alternative Berechnung geht nur über die Länge des Kiels. W=Kiellänge/1,9444444444 würde exakt den Wert von 54 Palmi zum Ergebnis haben. Ob Lavanha
davon Kenntnisse hatte, ist natürlich nicht bekannt. Er wird als Mathematiker sicher viele Optionen durchgerechnet haben.
Der zweite Decksbalken wurde laut Manuskript um 1/27 der Schiffsweite gekürzt. Das bedeutet, dass dort eine Weite von 52 Palmi erforderlich wird.
Die Weite des Flachs, also des Schiffsbodens, lies sich durch eine einfache Berechnung ermitteln. Flach=2/5*Schiffsweite. Das Ergebnis betrug 21,6 Palmi.
Um nun die vermeintlichen Kreisbögen für die Spantkontur zu ermitteln, bedarf es augenscheinlich einer etwas aufwendigeren Vorgehensweise. Stichpunktartige
kann festgehalten werden:
Die Schiffsweite wurde in fünf gleiche Abschnitte unterteilt.
Um den Schnittpunkt A/Basis mit (1/5*W)=R0 =10,8 Palmi einen Kreisbogen S-T-M schlagen.
R0=10,8 Palmi wird halbiert und bekommt die Bezeichnung Wh bei T.
R1=R0 wird durch den Schnittpunkt T/WH gezeichnet. Er schneidet alle zukünftigen Radien außer R4.
R2=R0 liegt ober- und unterhalb der Basis und wird durch N/Basis gezeichnet.
Der Schnittpunkt für den Mittelpunkt von R3=R0 wird wie folgt festgelegt:








